RLC Circuits

SERIES

RLC CIRCUITS The principles and formulas that have been presented in previous tutorials related to this section are used in all ac circuits. The examples given have been series circuits.

This section of the chapter will not present any new material, but will be an example of using all the principles presented so far. You should follow each example problem step by step to see how each formula used depends upon the information determined in earlier steps. When an example calls for solving for square root, you can practice using the square-root table by looking up the values given.

The example series circuit shown below will be used to solve for XL, XC, X, Z, IT, true power, reactive power, apparent power, and power factor.

The values solved for will be rounded off to the nearest whole number.

First solve for XL and XC.

Example RLC series circuit.

---

Now solve for X

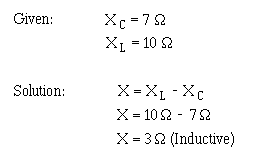
Use the value of X to solve for Z.

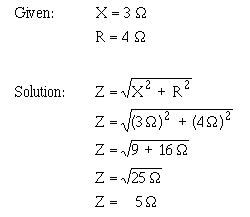
This value of Z can be used to solve for total current (IT ).

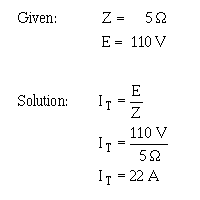
Since current is equal in all parts of a series circuit, the value of IT can be used to solve for the various values of power.

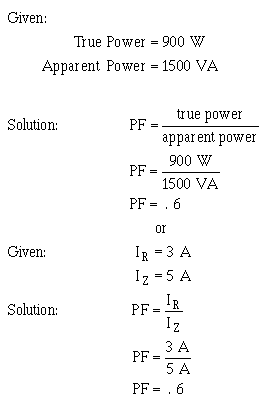
The power factor can now be found using either apparent power and true power or resistance and impedance. The mathematics in this example is easier if you use impedance and resistance.

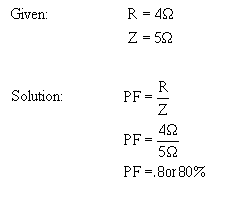
PARALLEL RLC CIRCUITS

When dealing with a parallel ac circuit, you will find that the concepts presented in this chapter for series ac circuits still apply. There is one major difference between a series circuit and a parallel circuit that must be considered. The difference is that current is the same in all parts of a series circuit, whereas voltage is the same across all branches of a parallel circuit. Because of this difference, the total impedance of a parallel circuit must be computed on the basis of the current in the circuit.

You should remember that in the series RLC circuit the following three formulas were used to find reactance, impedance, and power factor:

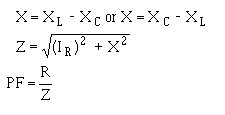
When working with a parallel circuit you must use the following formulas instead:

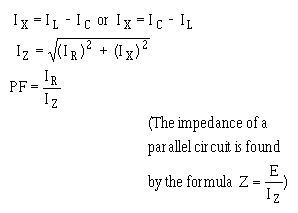
NOTE: If no value for E is given in a circuit, any value of E can be assumed to find the values of IL, IC, IX, IR, and IZ. The same value of voltage is then used to find impedance.

For example, find the value of Z in the circuit shown in the illustration below for a Parallel RLC circuit.

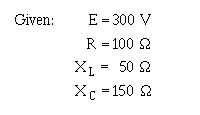
The first step in solving for Z is to calculate the individual branch currents.

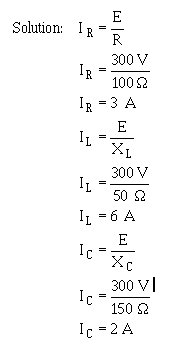
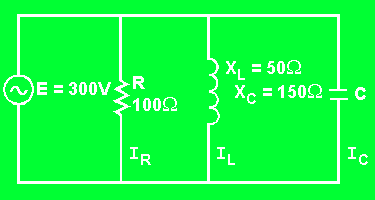
Parallel RLC circuit.

---

Using the values for IR, IL, and IC, solve for IX and IZ.

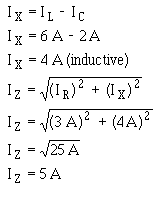
Using this value of IZ, solve for Z.

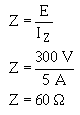
If the value for E were not given and you were asked to solve for Z, any value of E could be assumed. If, in the example problem above, you assume a value of 50 volts for E, the solution would be:

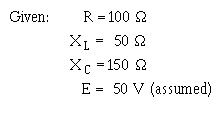
First solve for the values of current in the same manner as before.

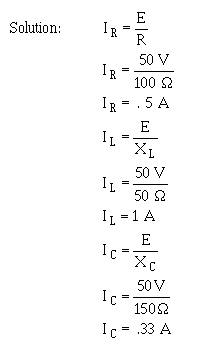
Solve for IX and IZ.

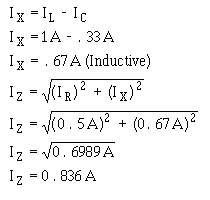
Solve for Z.

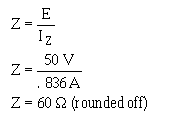
When the voltage is given, you can use the values of currents, I R, IX, and IZ, to calculate for the true power, reactive power, apparent power, and power factor. For the circuit shown (parallel RLC circuit, the calculations would be as follows.

To find true power,

To find reactive power, first find the value of reactance (X).

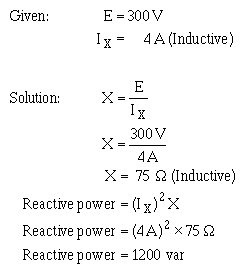
To find apparent power,

The power factor in a parallel circuit is found by either of the following methods.

(top) (return to homepage)