Transmission Lines cont

REFLECTIONS ON A TRANSMISSION LINE

Transmission line characteristics are based on an infinite line. A line cannot always be terminated in its characteristic impedance since it is sometimes operated as an OPEN-ENDED line and other times as a SHORT-CIRCUIT at the receiving end. If the line is open-ended, it has a terminating impedance that is infinitely large. If a line is not terminated in characteristic impedance, it is said to be finite.

When a line is not terminated in Z0, the incident energy is not absorbed but is returned along the only path available—the transmission line. Thus, the behavior of a finite line may be quite different from that of the infinite line.

REFLECTION OF DC VOLTAGE FROM AN OPEN CIRCUIT

The equivalent circuit of an open-ended transmission line is shown in the figure below, view A. Again, losses are to be considered as negligible, and L is lumped in one branch. Assume that (1) the battery in this circuit has an internal impedance equal to the characteristic impedance of the transmission line (Zi = Z0); (2) the capacitors in the line are not charged before the battery is connected; and (3) since the line is open-ended, the terminating impedance is infinitely large.

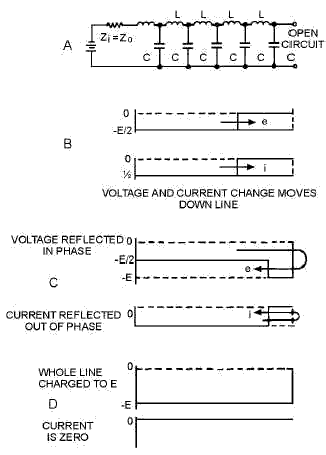
Reflection of an open ended line.

---

When the battery is connected to the sending end as shown, a negative voltage moves down the line. This voltage charges each capacitor, in turn, through the preceding inductor. Since Zi equals Z 0, one-half the applied voltage will appear across the internal battery impedance, Zi, and one-half across the impedance of the line, Z0. Each capacitor is then charged to E/2 (view B). When the last capacitor in the line is charged, there is no voltage across the last inductor and current flow through the last inductor stops. With no current flow to maintain it, the magnetic field in the last inductor collapses and forces current to continue to flow in the same direction into the last capacitor. Because the direction of current has not changed, the capacitor charges in the same direction, thereby increasing the charge in the capacitor. Since the energy in the magnetic field equals the energy in the capacitor, the energy transfer to the capacitor doubles the voltage across the capacitor. The last capacitor is now charged to E volts and the current in the last inductor drops to zero.

At this point, the same process takes place with the next to the last inductor and capacitor. When the magnetic field about the inductor collapses, current continues to flow into the next to the last capacitor, charging it to E volts. This action continues backward down the line until the first capacitor has been fully charged to the applied voltage. This change of voltage, moving backward down the line, can be thought of in the following manner. The voltage, arriving at the end of the line, finds no place to go and returns to the sending end with the same polarity (view C). Such action is called REFLECTION.

When a reflection of voltage occurs on an open-ended line, the polarity is unchanged. The voltage change moves back to the source, charging each capacitor in turn until the first capacitor is charged to the source voltage and the action stops (view D). As each capacitor is charged, current in each inductor drops to zero, effectively reflecting the current with the opposite polarity (view C). Reflected current of opposite polarity cancels the original current at each point, and the current drops to zero at that point. When the last capacitor is charged, the current from the source stops flowing (view D).

Important facts to remember in the reflection of dc voltages in open-ended lines are:

· Voltage is reflected from an open end without change in polarity, amplitude, or shape.

· Current is reflected from an open end with opposite polarity and without change in amplitude or shape.

Transmission line short

Standing waves

Reflection of AC voltage from a short circuit

Terminating a transmission line

Open Lines

Termination-in-Z0: termination in an open circuit, short circuit, capacitive circuit, and an inductive circuit

Termination in a resistance not equal to the characteristic impedance Z0

(top) (return to homepage)