Electrical Conductors

SQUARE MIL

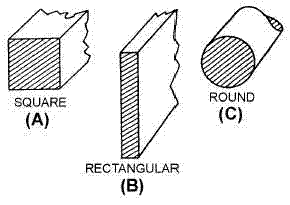
The square mil of electrical conductors is a unit of measurement used to determine the cross-sectional area of square or rectangular electrical conductors (views A and B of the illustration).

A square mil is defined as the area of a square, the sides of which are each 1 mil. To obtain the cross-sectional area of a square conductor, multiply the dimension of any side of the square by itself.

For example, assume that you have a square conductor with a side dimension of 3 mils. Multiply 3 mils by itself (3 mils ´ 3 mils). This gives you a cross-sectional area of 9 square mils.

Cross-sectional areas of conductors.

---

To determine the cross-sectional area of rectangular electrical conductors, multiply the length times the width of the end face of the conductor (side is expressed in mils).

For example, assume that one side of the rectangular cross-sectional area is 6 mils and the other side is 3 mils. Multiply 6 mils ´ 3 mils, which equals 18 square mils.

Here is another example. Assume that electrical conductors are 3/8 inch thick and 4 inches wide. The 3/8 inch can be expressed in decimal form as 0.375 inch. Since 1 mil equals 0.001 inch, the thickness of the conductor will be 0.001 ´ 0.375, or 375 mils. Since the width is 4 inches and there are 1,000 mils per inch, the width will be 4 ´ 1,000, or 4,000 mils. To determine the cross-sectional area, multiply the length by the width; or 375 mils ´ 4,000 mils. The area will be 1,500,000 square mils.

CIRCULAR MIL

The circular mil is the standard unit of measurement of a round wire cross-sectional area (view C of the illustration). This unit of measurement is found in American and English wire tables. The diameter of round electrical conductors (wire) used to conduct electricity may be only a fraction of an inch. Therefore, it is convenient to express this diameter in mils to avoid using decimals.

For example, the diameter of a wire is expressed as 25 mils instead of 0.025 inch. A circular mil is the area of a circle having a diameter of 1 mil, as shown in view B of of the illustration. The area in circular mils of a round conductor is obtained by squaring the diameter, measured in mils. Thus, a wire having a diameter of 25 mils has an area of 252, or 625 circular mils.

To determine the number of square mils in the same conductor, apply the conventional formula for determining the area of a circle (A = pr2). In this formula, A (area) is the unknown and is equal to the cross-sectional area in square mils, p is the constant 3.14, and r is the radius of the circle, or half the diameter (D). Through substitution, A = 3.14, and (12.5) 2; therefore, 3.14 ´ 156.25 = 490.625 square mils. The cross-sectional area of the wire has 625 circular mils but only 490.625 square mils. Therefore, a circular mil represents a smaller unit of area than the square mil.

A comparison of circular and square mils.

---

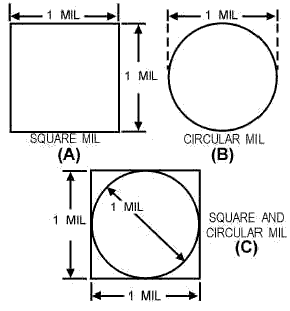
If a wire has a cross-sectional diameter of 1 mil, by definition, the circular mil area (CMA) is A = D2, or A = 1 2, or A = 1 circular mil.

To determine the square mil area of the same wire, apply the formula A = pr2; therefore, A = 3.14 ´ (.5) 2 (.5 representing half the diameter). When A = 3.14 ´ .25, A = .7854 square mil. From this, it can be concluded that 1 circular mil is equal to. 7854 square mil. This becomes important when square (view A of the second illustration above) and round (view B) electrical conductors are compared as in view C of the same illustration.

When the square mil area is given, divide the area by 0.7854 to determine the circular mil area, or CMA. When the CMA is given, multiply the area by 0.7854 to determine the square mil area. For example, Problem: A 12-gauge wire has a diameter of 80.81 mils. What is (1) its area in circular mils and (2)its area in square mils?

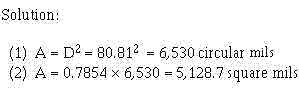
Problem: A rectangular conductor is 1.5 inches wide and 0.25 inch thick. What is (1) its area in square mils and (2) in circular mils? What size of round conductor is necessary to carry the same current as the rectangular bar?

A wire in its usual form is a single slender rod or filament of drawn metal. In large sizes, wire becomes difficult to handle. To increase its flexibility, it is stranded. Strands are usually single wires twisted together in sufficient numbers to make up the necessary cross-sectional area of the cable. The total area of stranded wire in circular mils is determined by multiplying the area in circular mils of one strand by the number of strands in the cable.

Circular-mil-foot of a conductor

Specific Resistance or Resistivity of a conductor

Wire sizes

Wire and cable

Factors governing wire sizes

Safe-current-ratings, copper vs aluminum conductors, and temperature coefficient.

Conductor-insulation, insulation resistance, dielectric strength, and types of insulation

Plastics: Varnished Cambric, Extruded Polytetrafluoroethylene, Fluorinated Ethylene Propylene, and Asbestos

Paper, silk and cotton, enamel, and mineral insulated cables and conductors

Conductor-protection: nonmetallic protection applications

Metallic-protection: types and applications of metallic protection of cables and wires

(top) (return to homepage)